Rendu par lancer de rayons par Xavier Michelon
Introduction
|
Après vous avoir présenté il y a quelques semaines les principes du rendu par algorithme de radiosité, je vous propose aujourd’hui d’aborder le lancer de rayon (raytracing en anglais). Nous garderons pour cette article la même approche que pour la radiosité : nous commencerons par quelques images types illustrant les principales caractéristiques de la méthode, puis nous étudierons le principes de l’algorithme de base (il en existe de nombreuses variantes). Les plus intéressés d’entre vous pourront se référer aux différents éléments de bibliographie que je vous livrerai en conclusion afin d’approfondir leurs connaissances. Historiquement, le lancer de rayon est la première méthode de rendu qui a permis d’approcher le réalisme photographique. Le terme de ‘lancer de rayons’ à été introduit en 1968 par Arthur Appel. Le moteur de rendu par lancer de rayon le plus connu est Povray, un logiciel libre qui a été porté sur la plupart des plates-formes informatiques passées et présentes. La plupart des moteurs de rendu actuellement ne sont pas basés sur le lancer de rayon, mais ils y font appel dès que l’on met en jeu la réflexion, la diffraction et la transparence que les algorithmes à base de Z-buffer ne savent pas gérer. |
 Image réalisée par André Pascual avec Moonlight Atelier |
Voici deux images représentatives de ce que permet d’obtenir un moteur de rendu par lancer de rayons. Ces deux images sont des rendus de scènes exemples contenues dans la distribution de PovRay.
|
Un vase se réfléchissant sur 2 murs |
|
Principe du lancer de rayons
|
Au cours de l’article concernant la radiosité, nous avons abordé le principe de dualité onde-particule de la lumière. Si la radiosité est basée sur l’aspect ondulatoire de la lumière, le ray-tracing est entièrement fondé sur une vision particulaire. Le principe de la vision est le suivant : Les sources de lumière (lampes, soleil…) émettent des rayons lumineux. Ces rayons viennent frapper les objets qui en réfléchissent une partie, en fonction de leurs propriétés physiques (« leur matériau »). Parmi tous les rayons lumineux, une partie va (directement ou après réflexion sur les objets) parvenir à l’oeil et former une image sur la rétine. Il serait illusoire de vouloir appliquer ce principe informatiquement. Une infime partie de la lumière émise parvient à l’oeil de l’utilisateur. La majorité de la lumière « se perd » dans la nature. La technique du lancer de rayon tente de reconstituer le parcours inverse de la lumière, en partant de l’oeil et en allant vers les sources. |
|
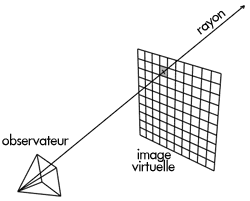
Pour cela, on place une image virtuelle dans la scène devant l’observateur (c’est cette image qui s’affichera sur votre écran). Pour chacun des pixels qui constituent l’image, on lance un rayon partant du point de vue (l’observateur) passant par le pixel (son centre ou un autre point au hasard). La couleur de pixel traversé va être déterminée en suivant le cheminement du rayon lancé jusqu’aux sources lumineuses de la scène 3D.
|
Pour chaque rayon lancé de l’oeil, on calcule le premier objet qu’il intersecte, ce qui implique un parcours de l’ensemble des faces de la scène. Au niveau légèreté, on a déjà vu mieux ;). Heureusement, il existe des techniques d’optimisation qui permettent de limiter le nombre de tests. Une fois le premier objet trouvé, il faut déterminer la couleur du pixel à afficher. Cette couleur dépend du matériau de la face, et bien sûr de l’éclairage. Aussi faut il déterminer quelles sont les sources lumineuses qui éclairent le point. Pour cela, on relance des rayons issus du point du point considéré vers chacune des sources lumineuses de la scène. Si ce rayon parvient à la source sans intersecter d’autre objet, alors la source contribue à l’éclairage du point. Sinon, un objet masque la source, et un effet d’ombre et engendré naturellement. |
|
La figure 2 est une vue de dessus du cheminement du rayon. Le rayon R1 provient de l’oeil, disons pour le pixel (x,y). Il heurte la face F1 au point p. Pour déterminer l’éclairage du pixel (x,y). Les rayons lancés de p montrent que la source S1 va contribuer à l’éclairage de P, mais que S2 est masquée par F2. La face F2 va porter son ombre sur F1.
Dans le cas où le rayon lancé depuis le point de vue n’intersecte aucun objet, le pixel (x,y) considéré prend une valeur « de fond », qui peut être soit une couleur fixe, soit la couleur du pixel (x,y) d’une image.
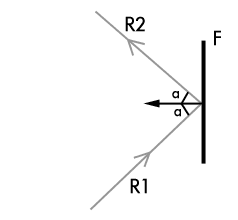
Supposons à présent qu’on souhaite gérer les effets de réflexion. Lorsqu’un rayon issu du point de vue vient frapper une face définie comme réfléchissante, on détermine la couleur du point en lançant un rayon vers les sources, comme nous l’avons vu précédemment, mais également en lançant un rayon spéculaire qui va permettre de prendre en compte la réflexion. La direction de rayon spéculaire est dicté par la loi de Descartes concernant la réflexion :
|
Le Rayon R1 se réfléchi en rayon R2 sur la face F de façon à ce que l’angle entre R1 et la perpendiculaire à F soit égal à l’angle entre R2 et cette même perpendiculaire. Une fois le rayon spéculaire déterminé, on effectue le même calcul que pour le rayon initial : on recherche la première face intersectée par le rayon, on lance un rayon vers chacune des sources….. La face frappée par R2 peut elle-aussi être réfléchissante, auquel cas on réitère le processus de réflexion en lançant un rayon spéculaire supplémentaire. L’implémentation de ce principe en machine est facile en utilisant des algorithmes récursifs. La couleur qui sera finalement attribuée au pixel (x,y) est un mélange de la lumière directement incidente sur la face et de la couleur de réflexion obtenue par le calcul expliqué ci dessus. Ce mélange dépend évidemment des propriétés de réflexion des objets. Nous ne faisons ici qu’aborder le principe du lancer de rayon, aussi je ne vous donne pas de formules. Vous les trouverez dans les ouvrages cités en conclusion. |
|
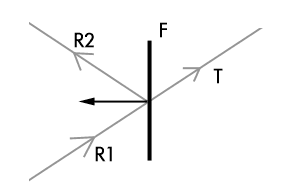
Pour la transparence, l’idée est la même que pour la réflexion, on lance un rayon supplémentaire, dit rayon « transmis ». La valeur finale de la couleur du pixel est obtenue en mélangeant les couleur calculées à partir de l’éclairage direct, de la réflexion et de la transparence, en fonction des propriétés du matériau.
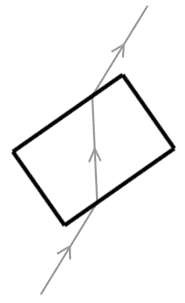
| Le lancer de rayon permet également pour les objets transparents de reproduire le phénomène de diffraction. L’exemple le plus classique de diffraction est la déformation des objets vus à travers un verre ou une bouteille. La diffraction est régie par les lois de Descartes, et est liée au fait que la propagation de la lumière varie en fonction du milieu traversé. La figure 5 illustre le cheminement d’un rayon lumineux transmis lors de la traversée d’un matériau transparent tel que le verre. |
|
Figure 5 : le phénomène de diffraction
La méthode du lancer de rayons permet d’obtenir des résultats de très grande qualité et est capable de recréer des phénomènes physiques que les autres méthodes de rendu ne peuvent reproduire. Mais le prix à payer est un temps de calcul bien plus long qu’avec le tampon de profondeur, qui fait office de référence en terme de vitesse.
Développé depuis de nombreuses années, les algorithmes de lancer de rayons ont fait l’objet de nombreuses recherches qui ont abouti à des améliorations notables de la méthode.
Voici pour terminer deux références bibliographiques qui vous permettront ,si vous le souhaitez, d’appronfondir le sujet en vous plongeant dans les formules et algorithmes qui y sont proposés. Et qui sait, vous parviendrez peut être à écrire votre propre ray-tracer !
|
La synthèse d’image
|
B. Péroche & Al.
|
Hermes
|
| Cet excellent ouvrage en français constitue une bonne porte d’entrée sur le monde de l’infographie, et la partie consacrée au ray-tracing est bien faite. | ||
|
An Introduction to Ray-Tracing
|
A.S. Glassner & Al.
|
Morgan Kaufmann
|
| Une collection de textes (en anglais) écrits par de grands spécialistes du raytracing. Le livre à plus de 10 ans, mais le contenu est toujours valide ! | ||